You might still remember the times when you played Tic-Tac-Toe (a.k.a. noughts and crosses) in your childhood:

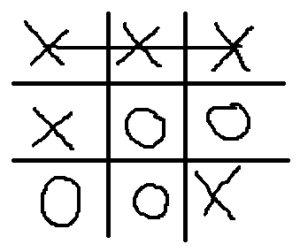
In a series of blog posts I want to apply neural networks on this well-known game. But before we may do that, we need to do some preparations.

Eventually, we want to teach a neural network to determine:

• if a board has a winner,
• who the winner is, and
• after which move the winner has won the board.

To be able to properly describe such a board, we need to define an order on the board. I decided to take the order “top-left to bottom-right” like this:

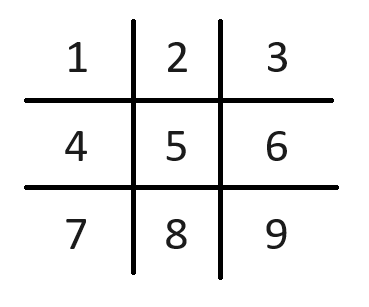
You may also apply a different, more sophisticated scheme for defining the position, but let’s keep it simple.

With this nomenclature, we now can describe the board mentioned initially using a set of integers: 1,6,9,5,4,7,3,8,2. Even more interesting this become, if you consider this not being a set but a list (including order). That is important, because a board may have two “winners”, depending on which player came first. Note that

• by definition, let us assume that X starts the game,
• every other round, it is the other’s player to move (even positions are ‘O’ moves, odd positions are ‘X’ moves), and
• that there are always exactly nine positions in total until the board is fully populated (also called an assignment).

Moreover, the list must not have any duplicates: 1,1,1,1,1,1,1,1,2 may also be a list of numbers, but this does not describe a proper Tic-Tac-Toe game, because the position 1 appears more than once. Therefore, the generation of the list represents a system of choosing without repetition. That brings us to another aspect: We first need to determine, if a list of integers is a valid board after all.

[to be continued on the next page]

Training neural networks means that you

• need a lot of data, and
• you need to run a regression model applying backpropagation

To be able to do that, we need to generate all possible combinations and store them for training and evaluation later on.

Here is a Jupyter notebook with a data generator, which exactly does this:

  tic-tac-toe-datagenerator.zip (1.7 KiB, 121 hits)

Essentially this notebook does:

1. Generate all possible assignments of nine positions with values from the range [1..9] (with repetition),
2. Determine which of those assignments are without repetition (then called “valid board”),
3. Determine if there is a winner,
4. Determine who is the winner,
5. Determine after which move the winner was clear.

The result is stored in a gzipped¹ text file called tictactoe.txt.gz, which will have an approximated size of 915MB (compressed!). Uncompressed, it yields a size of a little below 2GB.

Each line of the text file looks something like this:

123456789 1104

whereas the first nine digits represent the list (here: 1,2,3,4,5,6,7,8,9) of moves. The following block of four digits (separated with a space from the list) have the following meaning:

1. The first “1” stands for “this is a valid board”. If the list was not a valid board, it would read “0” (and all subsequent digits would be irrelevant.
2. The second “1” stands for “there is a winner”. If there was no winner (and the outcome of the game was a tie), this position would have a “0”.
3. The third digits (“0”) represents the winner. In case “X” has won the game, “0” is provided. If “O” had won the game, “1” is provided.
4. The last digit (“4”) specifies after which move (of both having done their part) the outcome of the game was clear; the value “4” here means that after the fourth move of the winner (here “X”), that is after having occupied position 7, the player has won.
   If the board was a tie, we define this field to contain the digit “9” to indicate that even after the last position was filled.

In total there are

• 9⁹ lines in the file representing (=387,420,489) ² assignments,
• out of these, 362,880 are valid boards (=9!)³, that is roughly 0,1%,
• out of these, 127,872 are won by X ⁴.
• Another 34,560 are won by Y ⁵.
• Therefore, there are 162,432 boards, which either party has won.
• There are 200,448 games ending in a tie ⁶.

Note that we do not have any duplicate games in the dataset.

To simplify (and speed up processing), the jupyter notebook also generates a second file called tictactoe_valid.txt (without gzip compression), which only contains the valid boards. This file has a size of roughly 5.4MB.

Equipped with these preparations, we can tackle our neural networks now.

Footnotes

1. The text is very repetitive. GZIP, even with “highest compression” mode has still some troubles to remove all redundancies. Therefore, other compression algorithms might be suited better. However, for the sake of brevity, this drawback is accepted here. ↩︎
2. You may verify this by running zcat tictactoe.txt.gz | wc -l ↩︎
3. You may verify this by running zcat tictactoe.txt.gz | egrep ' 1' | wc -l ↩︎
4. You may verify this by running zcat tictactoe.txt.gz | egrep ' 110' | wc -l ↩︎
5. You may verify this by running zcat tictactoe.txt.gz | egrep ' 111' | wc -l ↩︎
6. You may verify this by running zcat tictactoe.txt.gz | egrep ' 10' | wc -l ↩︎