In our previous blog, we saw that it is possible to provide multiple outputs, each one for a specific use case. So far, the two binary use cases, winning and winner, and the categorical use case, move, do not have any mutual dependencies between them: Their result are all derived from the original inputs.
Let’s now see, if stacking the layers may help to reduce the model’s complexity whilst still getting the same outputs with the same quality (accuracy = 1.0).
For that we will use the exact same environment as in our previous post, but we will change the model’s layout significantly:
inputs = keras.Input(shape=(9))
normalized_inputs = normalizer(inputs)
# Move block
move_dense1 = keras.layers.Dense(80, activation='relu')
move_dense2 = keras.layers.Dense(120, activation='relu')
denseMoveOutput = keras.layers.Dense(4, name="move_output")
move = denseMoveOutput(move_dense2(move_dense1(normalized_inputs)))
# winner block
winner_dense = keras.layers.Dense(40, activation='relu')
denseWinnerOutput = keras.layers.Dense(1, name="winner_output")
winner = denseWinnerOutput(winner_dense(normalized_inputs))
# Winning block
winning_input = keras.layers.Concatenate()
winning_dense = keras.layers.Dense(16, activation='relu')
denseWinningOutput = keras.layers.Dense(1, name="winning_output")
winning = denseWinningOutput(winning_dense(winning_input([move, winner])))
model = keras.Model(inputs=inputs, outputs=[winning, winner, move], name="tictactoe_model")
print(model.summary())This will give us a rather complex model summary:
Model: "tictactoe_model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, 9)] 0 []
normalization (Normalization) (None, 9) 19 ['input_1[0][0]']
dense (Dense) (None, 80) 800 ['normalization[0][0]']
dense_1 (Dense) (None, 120) 9720 ['dense[0][0]']
dense_2 (Dense) (None, 40) 400 ['normalization[0][0]']
move_output (Dense) (None, 4) 484 ['dense_1[0][0]']
winner_output (Dense) (None, 1) 41 ['dense_2[0][0]']
concatenate (Concatenate) (None, 5) 0 ['move_output[0][0]',
'winner_output[0][0]']
dense_3 (Dense) (None, 16) 96 ['concatenate[0][0]']
winning_output (Dense) (None, 1) 17 ['dense_3[0][0]']
==================================================================================================
Total params: 11,577
Trainable params: 11,558
Non-trainable params: 19
__________________________________________________________________________________________________
NoneNote that the number of trainable parameters has dropped significantly: While we were at around 23-28k parameters, this model only has around 12k trainable parameters.
May be it is easier to digest this complex model with the following graphical representation:
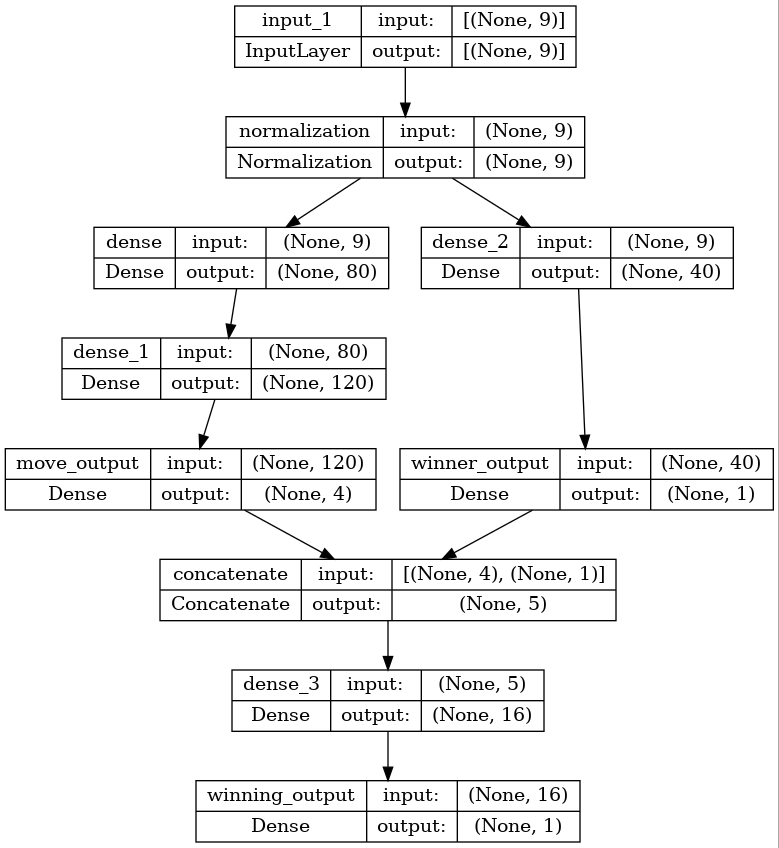
Essentially, the following logic is behind this layout:
- From our previous blog posts we know that for a Dense layer model, it is easier to solve the use cases “move” (categorical, which move caused that a player has won the game) and “winner” (binary, which player is the winner) than the “winning” one (is there a winner at all). Note that winner may have false friends: It may be ambiguous in case that there is no winner at all (and the game ended in a tie).
- For these two cases, we had determined that a 80/120 Dense layer stack, respectively a single 40 Dense layer was sufficient.
- In the model above, we exactly do the same: We calculate both outputs in parallel. Finally, there is move respectively a winner output layer without any activation function in place. Our loss functions for move and winner will also consume these “intermediate outputs”.
- For calculating the “winning” case (there is a real winner at all, i.e. we did not end up in a tie), we do not refer to the inputs anymore, but provide a simple Dense layer with 16 units only, combining (that is: concatenating) the outputs of the two use cases “move” and “winner”.
- In the previous sensitivity analysis, the winning use case was the most complex use case to determine of all three. It alone took 13.3k parameters to reliably determine the result with an accuracy of 1.0
If we now run this model through training and evaluation, we will get
[...]
Epoch 45/100
567/567 [==============================] - 4s 7ms/step - loss: 0.0029 - winning_output_loss: 3.0598e-06 - winner_output_loss: 0.0027 - move_output_loss: 2.3709e-04 - winning_output_accuracy: 1.0000 - winner_output_accuracy: 1.0000 - move_output_accuracy: 1.0000 - lr: 0.0036and an evaluation accuracy of
284/284 [==============================] - 3s 8ms/step - loss: 0.0028 - winning_output_loss: 2.5878e-06 - winner_output_loss: 0.0026 - move_output_loss: 2.2907e-04 - winning_output_accuracy: 1.0000 - winner_output_accuracy: 1.0000 - move_output_accuracy: 1.0000
[0.002793017541989684, 2.5877923235384515e-06, 0.002561361063271761, 0.0002290689299115911, 1.0, 1.0, 1.0]This model can be downloaded here:
tic-tac-toe-Multistacked-Model.zip (113.5 KiB, 138 hits)
This implies that we have found a model, which reliably returns answers to all three use cases, but is significantly smaller than the smallest model of the most complex use case (“winning”). Essentially, we used logical dependencies between the three use cases, which helped us to optimize our model. However, it should not go unnoticed that this also meant that we have made the model more specific: It cannot be reused for another game anymore, which would not yield this kind of logical dependency between the use cases.
For your reference, the Jupyter notebook can be downloaded here:
tic-tac-toe-Multistacked-notebook.zip (74.7 KiB, 71 hits)